A cache is a in-memory data structure which is designed for fast access, insertion and deletion.
All caches have memory limit which requires cache eviction policy. Whenever the memory of cache is full, we use a cache eviction policy to delete an item to make space for the new item.
Today we’re going to look at how to design a cache which uses Least Recently Used as its cache eviction policy.
There are many cache eviction policies:
- First In First Out
- Most/Least Recently Used
- Most/Least Frequently Used
- Random Replacement
What’s LRU ?
LRU is a cache eviction policy in which we remove the Least Recently Used item. Here Least Recently Used means the item that was accessed least recently.
A cache supports following operations:
1. Insert(item)
Inserts an element into the cache. If the cache is full then the Least Recently Used item is deleted to make space for the new item.
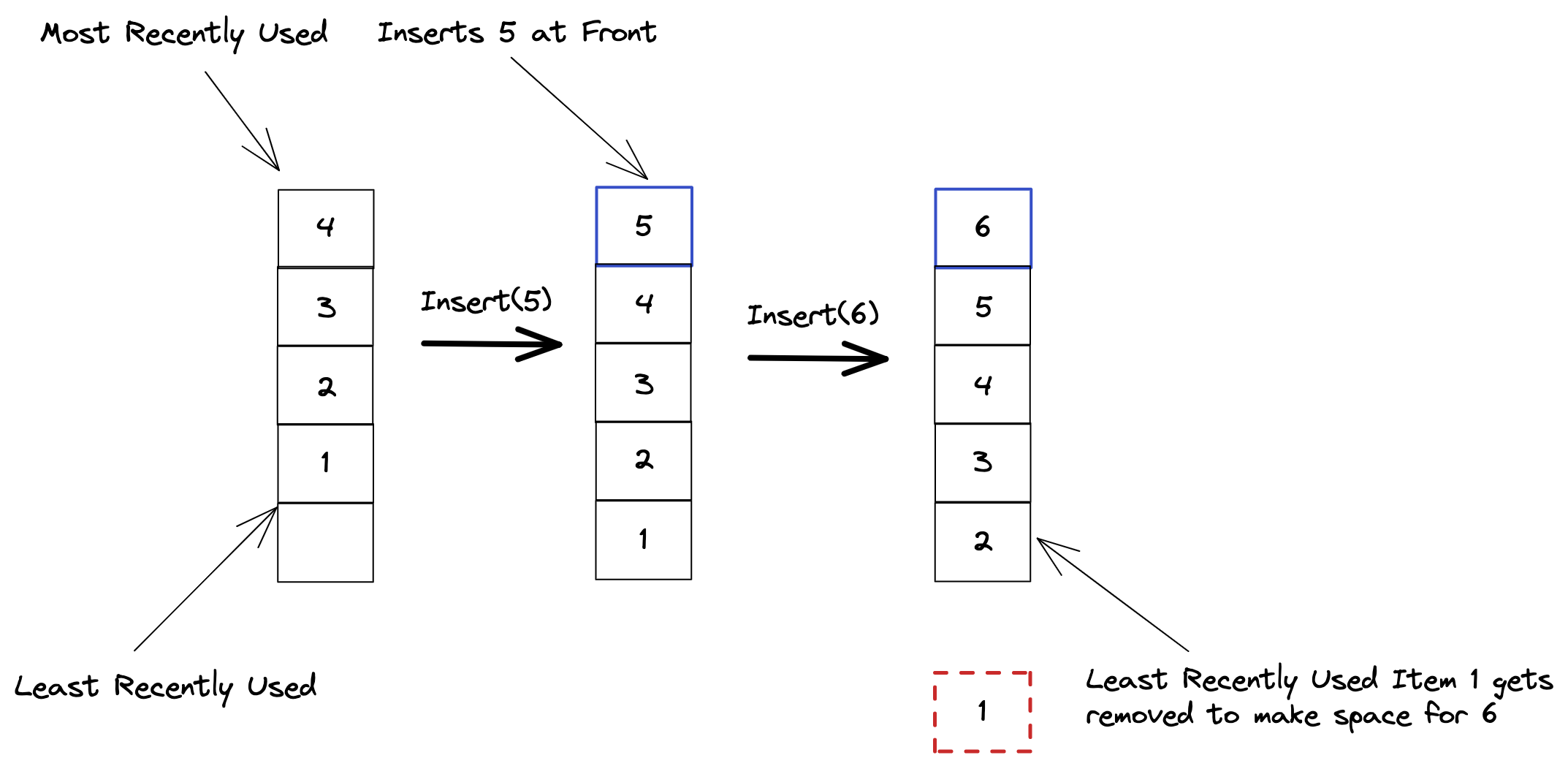
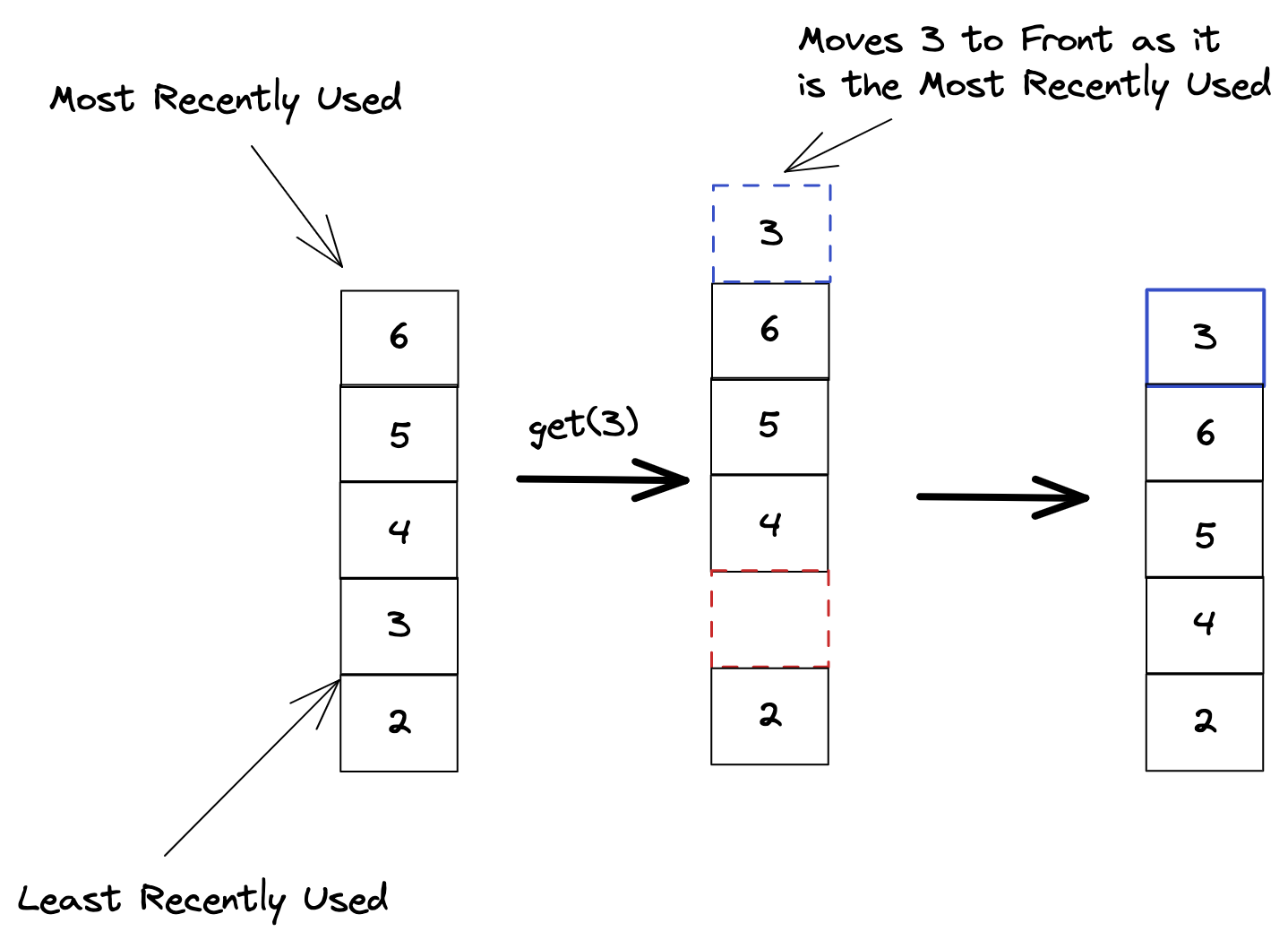
2. Get(item)
Retrieves an item from the cache. The accessed item becomes the most recently used item.
3. Delete(item)
Deletes an item from the cache.
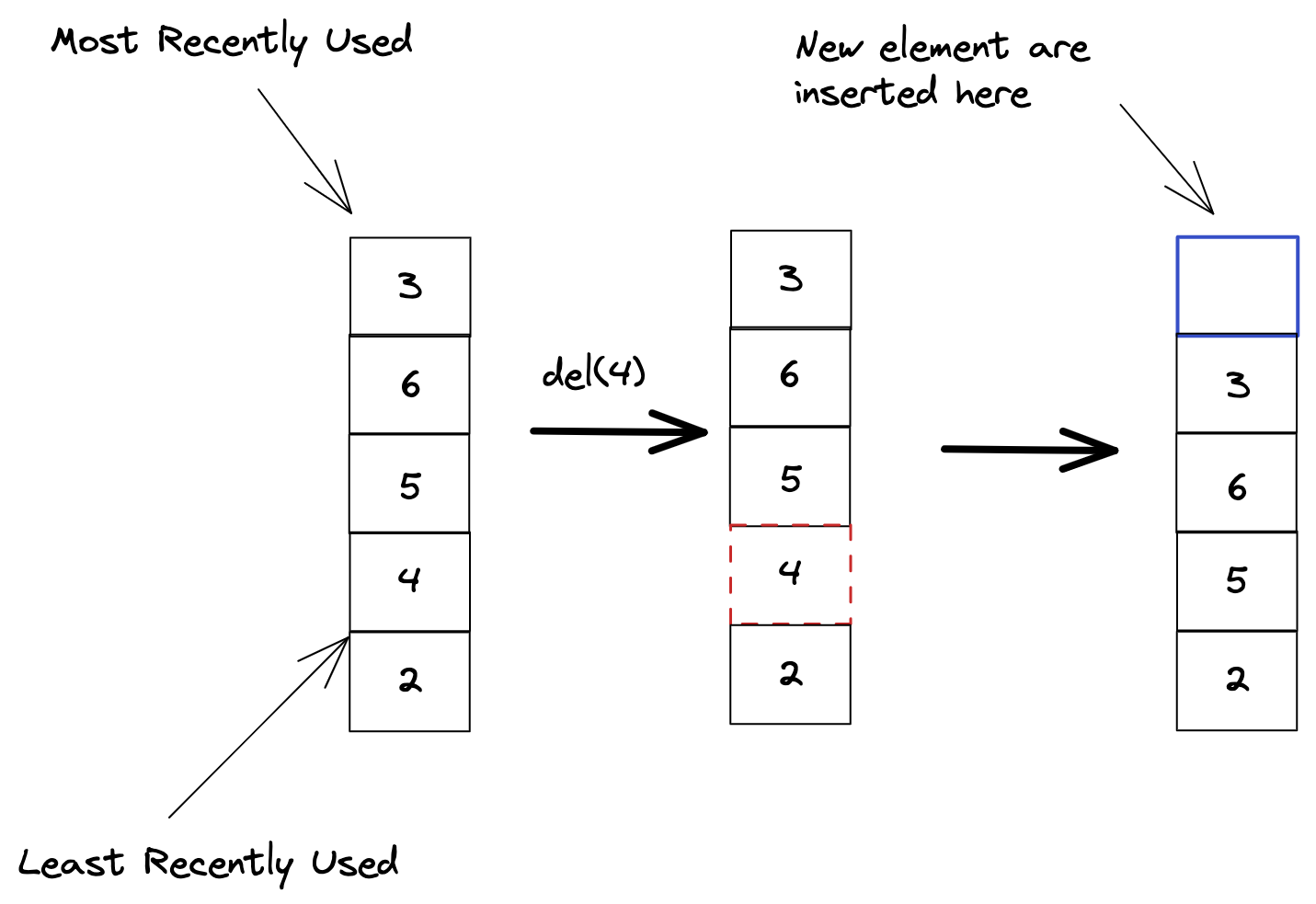
Since we’re implementing a cache these operations must run in constant(O(1)) time. Now how to achieve that ?
How to LRU ?
Making insert(item) O(1)
If we observe insert carefully we can see that it’s is similar to a Queue.
What’s a Queue ?
A Queue allows inserting elements(enqueue) at the front and removing elements(deque) from the rear. enqueue/dequeue can be performed in O(1) time.
On insertion item is added to the rear(most recently used). If the memory is full one item is dequeued from the front(least recently used) to make space for the new item.
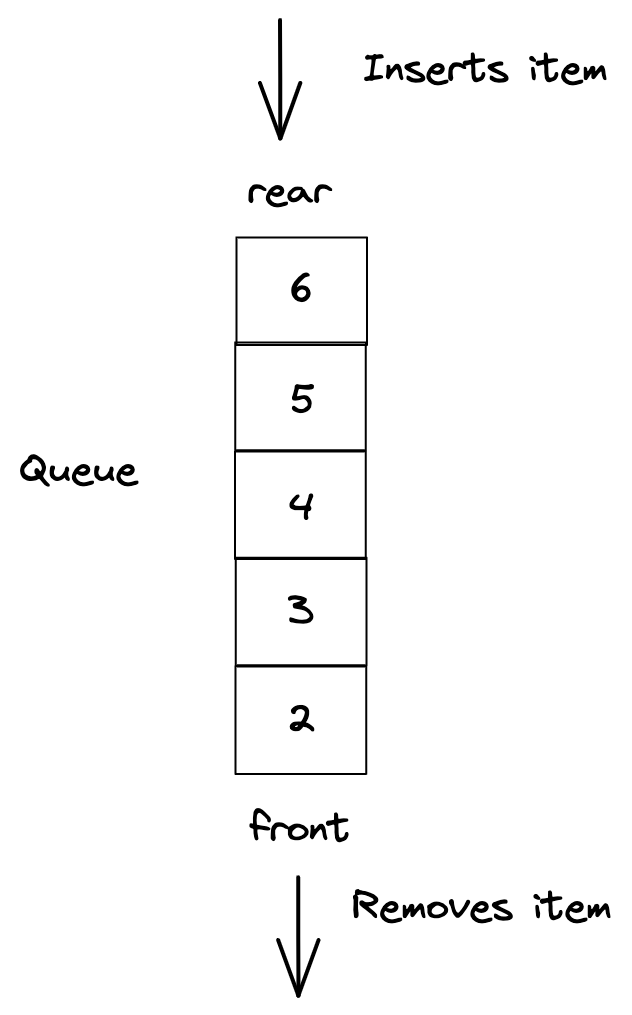
Queue solves insert(item) in O(1). Next let’s see get(item).
What about get(item) ?
Queue solves inserting elements, however it doesn’t solve get(item) in O(1). Getting an element in a queue requires to scan the whole queue which will take O(N) time. Not what was intended.
So how to perform get(item) in O(1) ?
We need to access an item in O(1) time. What data structure can do that ? Yes, HashMap.
Using HashMap we can access any item in O(1) time.
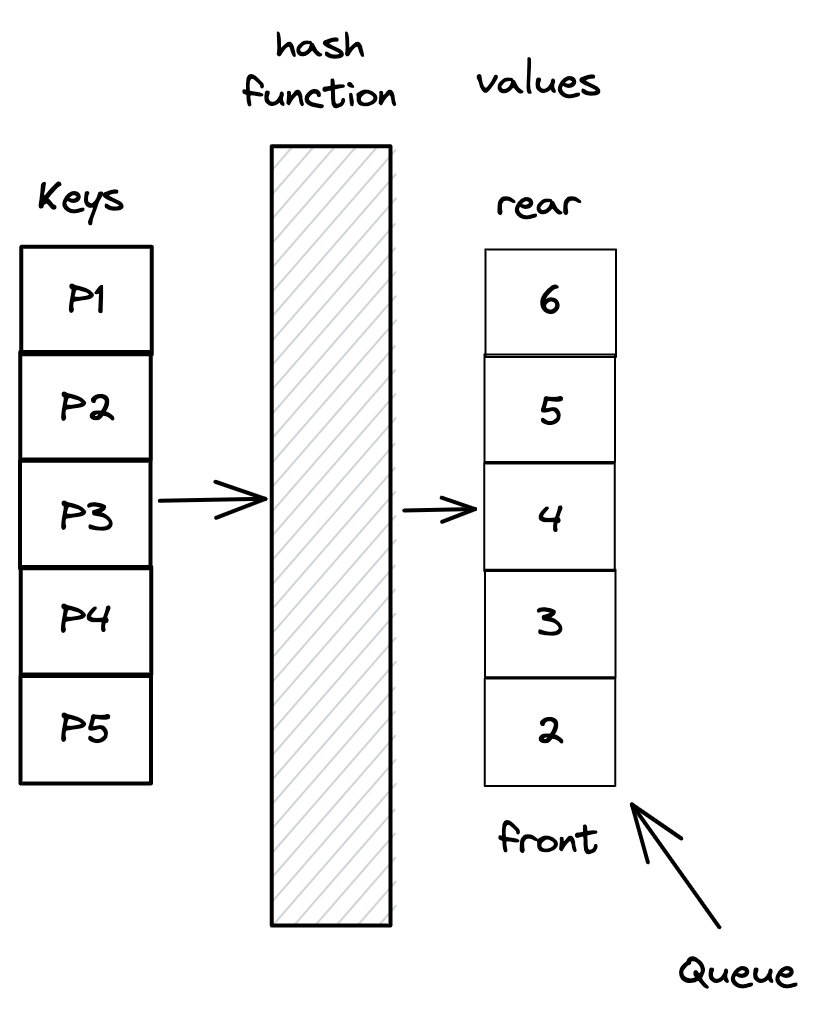
However, did this solve the problem ? We can access any item in O(1) time but is get(item) O(1) ? The answer is No.
Remember get(item) has 2 steps:
- Access the item.
- Mark the accessed item as Most Recently Used.
For the 2. step we’ll need to move the item to the rear. This will take O(N) time.
Why will it take O(N) ?
Right now queue is represented as an array. Shifting the accessed item will require O(N) time to shift the elements.
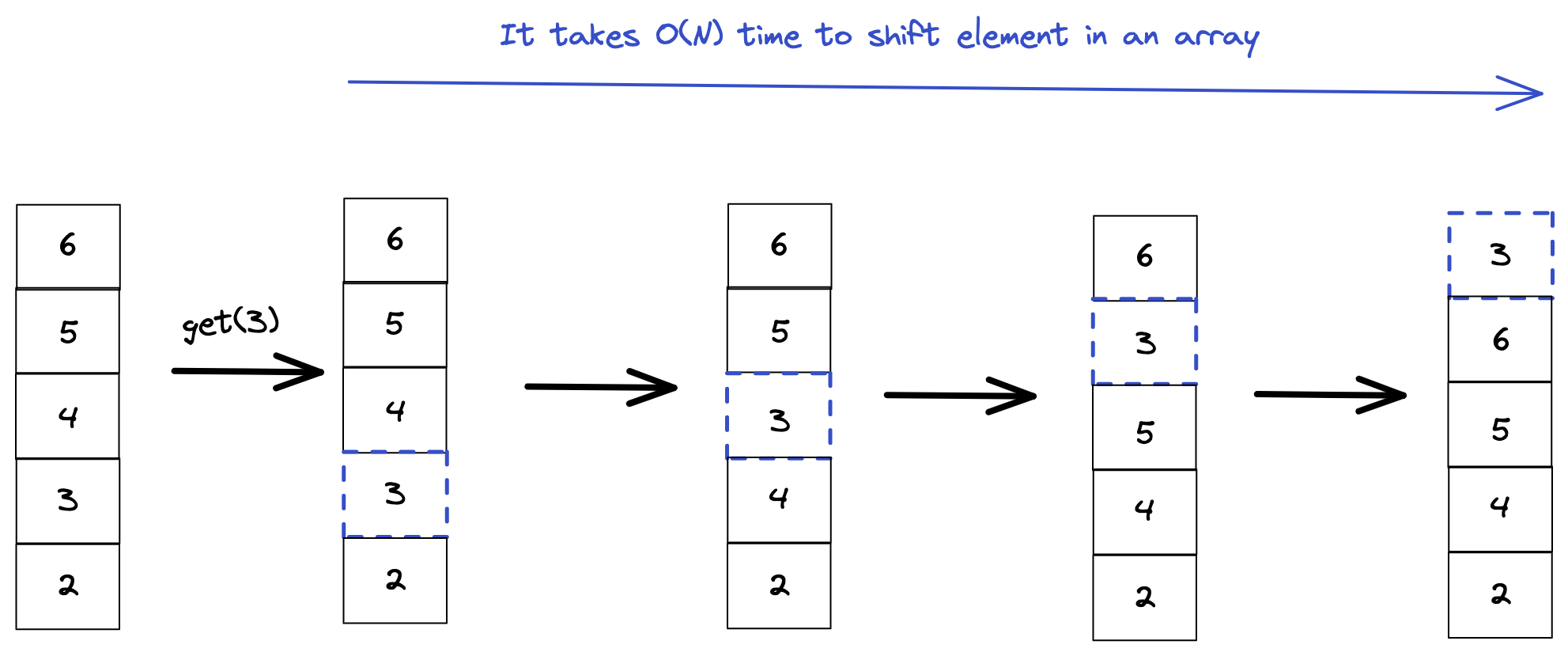
How can we reduce time to O(1) ?
Making get(item) O(1) ?
The issue here is that we’re using an array. We need a data structure where shifting an element takes O(1) time.
What if we use Doubly Linked List. Will that help ?
Doubly Linked List requires O(1) to shift any item. This is because we only need to change the pointers of the item being accessed.
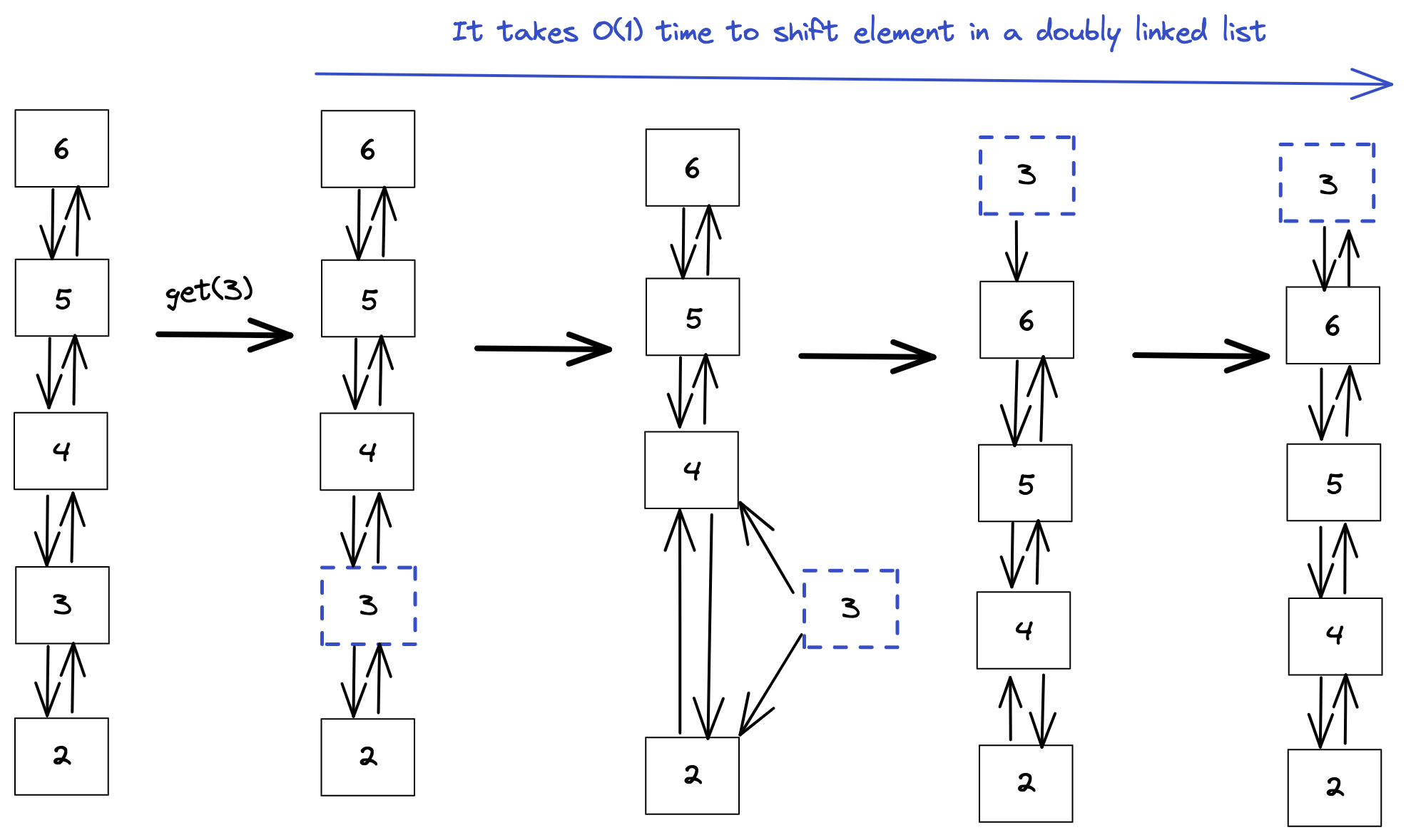
So now we’ve O(1) get(item) and insert(item). Let’s see how much time del(item) takes ?
How about del(item) ?
Using Doubly Linked List makes deleting an item O(1) since we only need to delete the pointers of the deleted item and link the previous and next element of the item.
Finally our cache looks like this
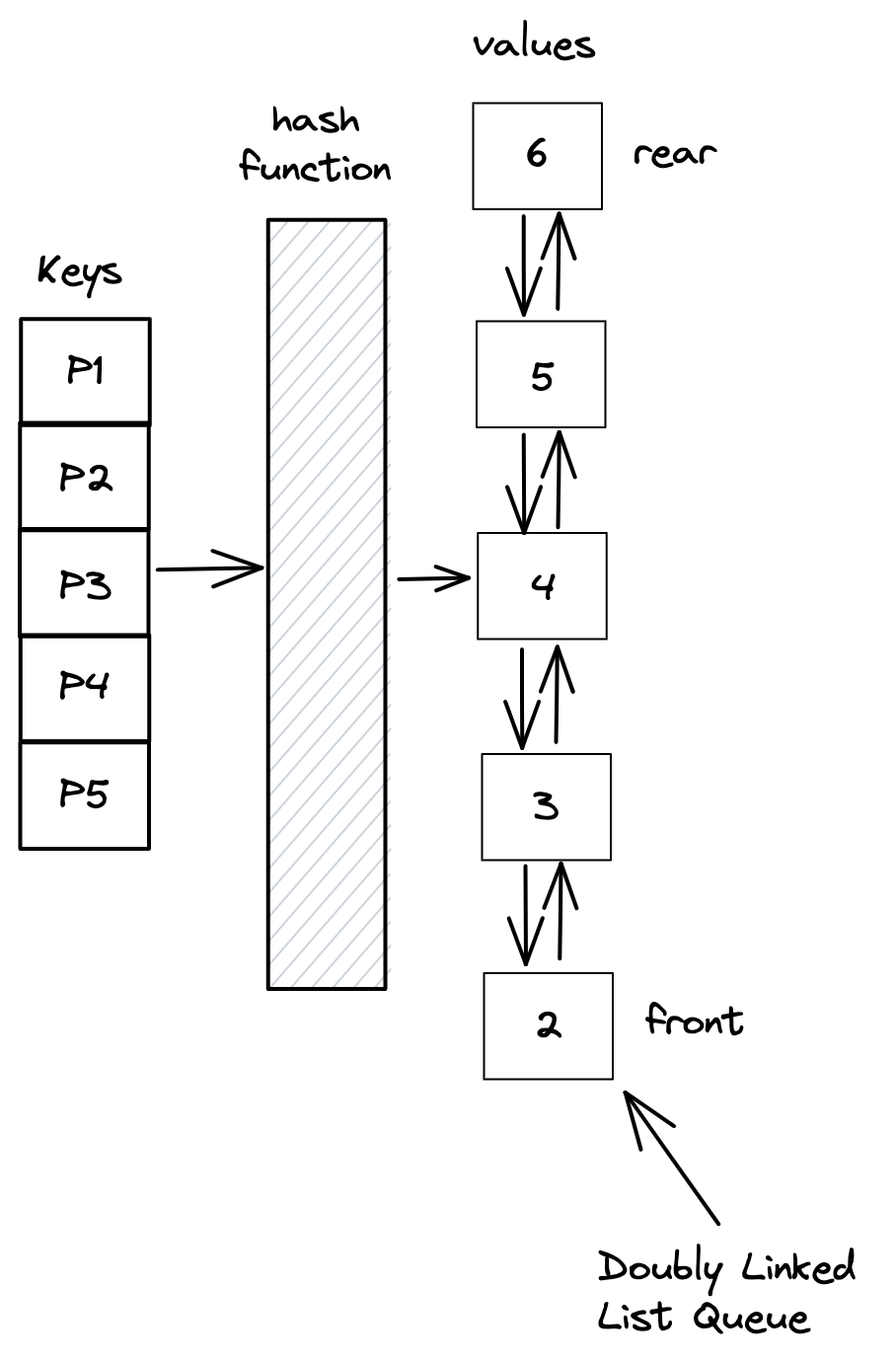
This LRU design performs insert(item), get(item) and delete(item) in O(1) time.