Binary Search Tree

A Binary Search Tree or a BST is a tree whose inorder traversal is sorted. For each node in a BST the left subtree has values smaller the node’s value and the right subtree has values greater than the node’s value.

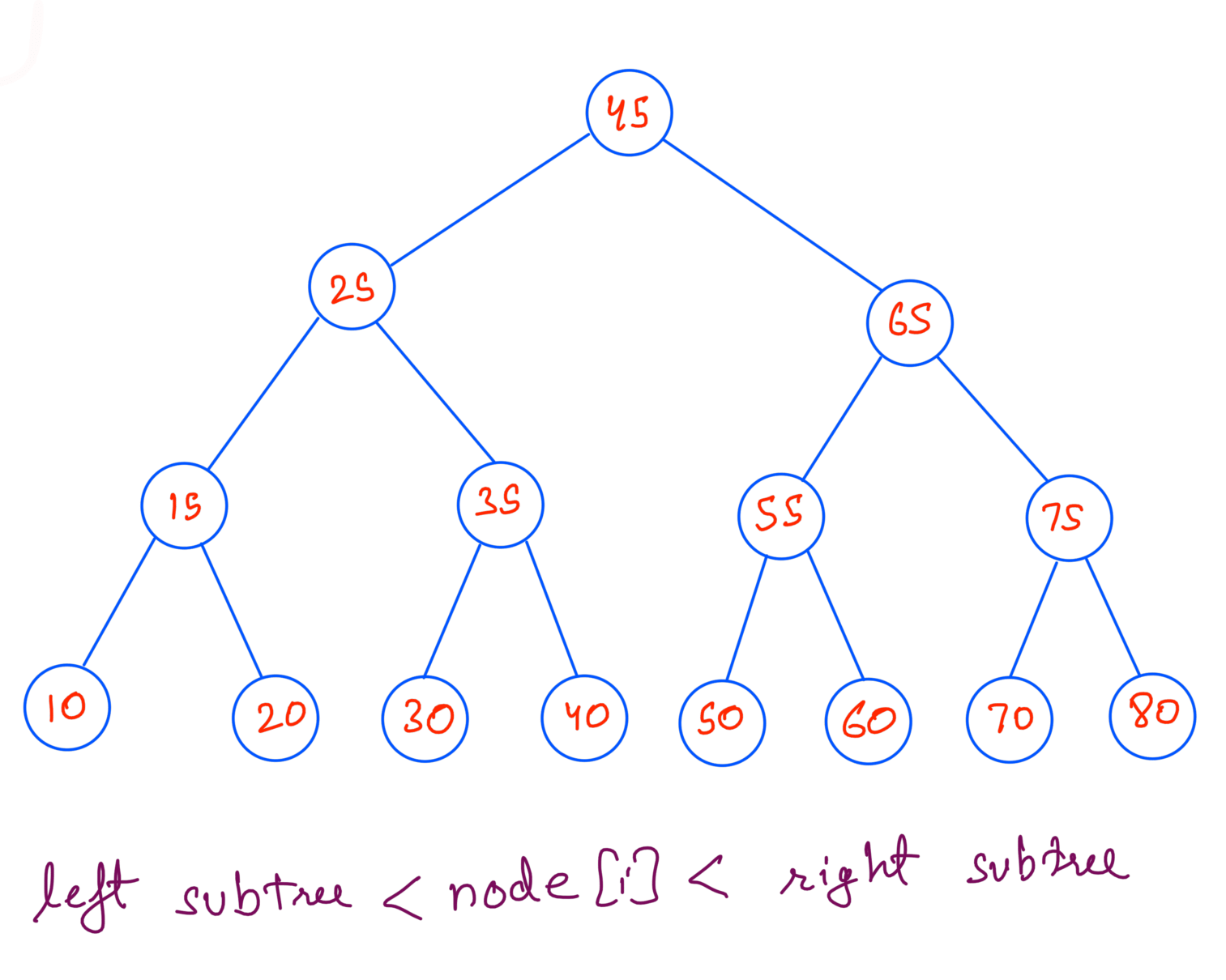
Search in a BST

Since in a BST the values lesser than the current node lies in the left subtree and greater values lies in the right subtree. We can use this property to search for a value.

At each node we’ve to check:

• if the value is lesser than the current node’s value. Go to left child as values lesser than the current node are present in left subtree.
• if the value is greater than the current node’s value. Go to right child as values greater than the current node are present in right subtree.
• if the value is equal to the current node than we’ve found the value.

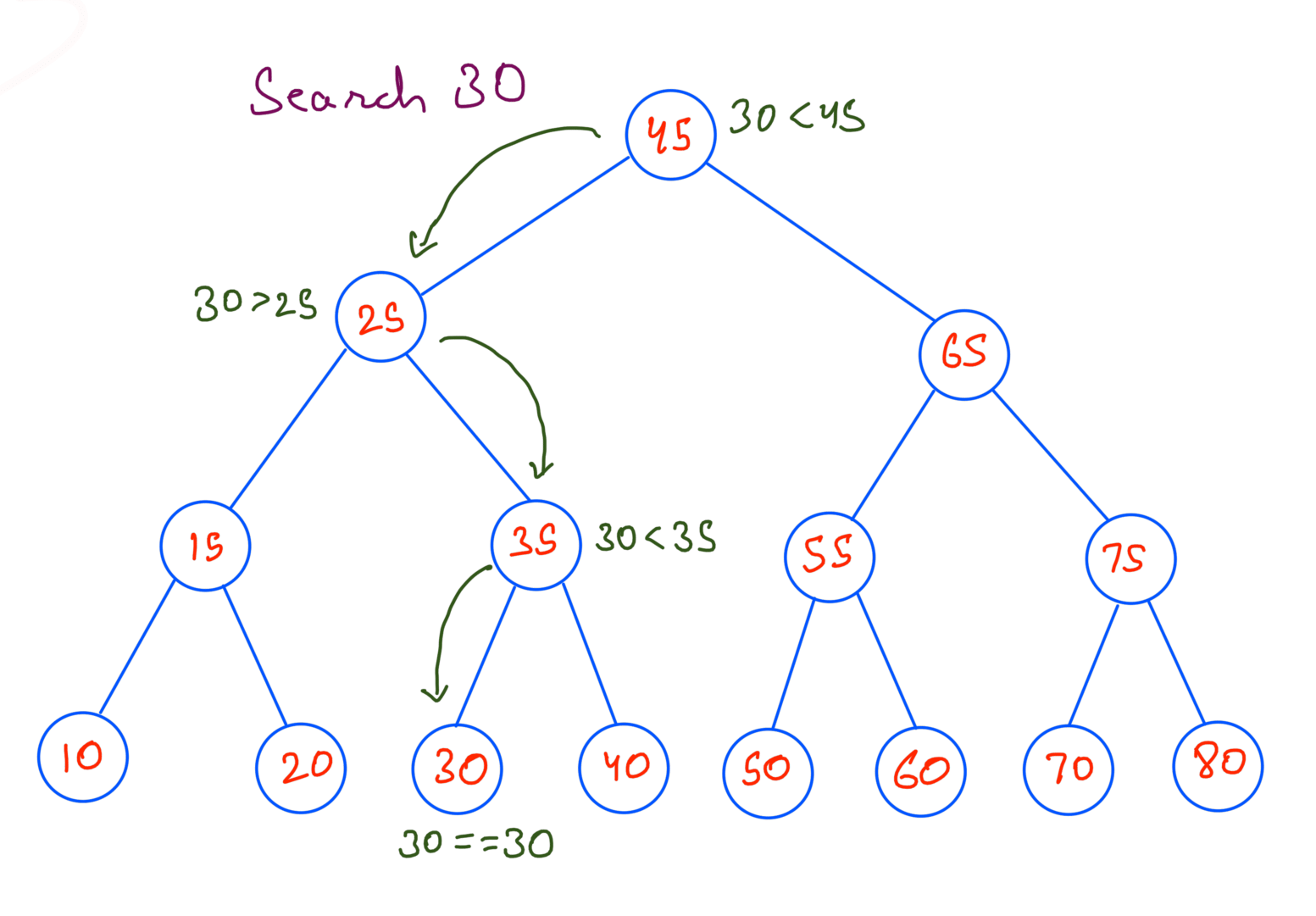
Here’s how it’ll work:

This can be implemented using recursion:

def search(root, val):
  if not root:
    return None
  elif val < root.val:
    return self.search(root.left, val)
  elif val > root.val:
    return self.search(root.right, val)
  elif val == root.val:
    return True

The Time Complexity for this code when BST is completely balanced is O(logN). This can be verified by looking at the example for searching 30. There are 4 lookups needed for searching 30 which is equal to log(15) = 4.

However the worst case Time Complexity will be O(N). A BST is not necessarily balanced. Here’s how searching looks like in a skewed BST:

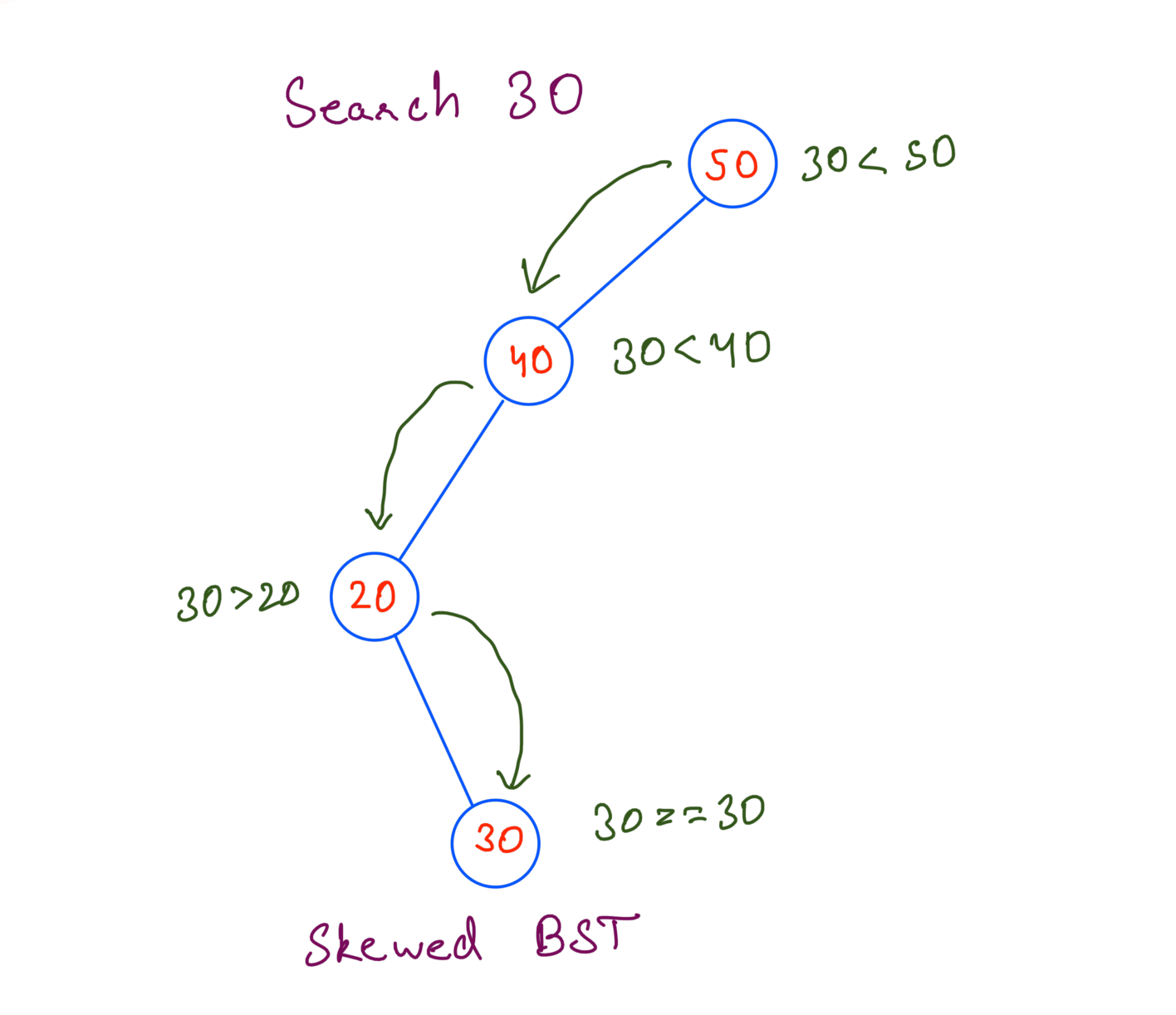
In a Skewed BST we’ve to go through all the nodes to search 30.

To make sure the TC is always O(logN) we can use Balanced Tree data structures like Black-Red Tree or AVL Tree.

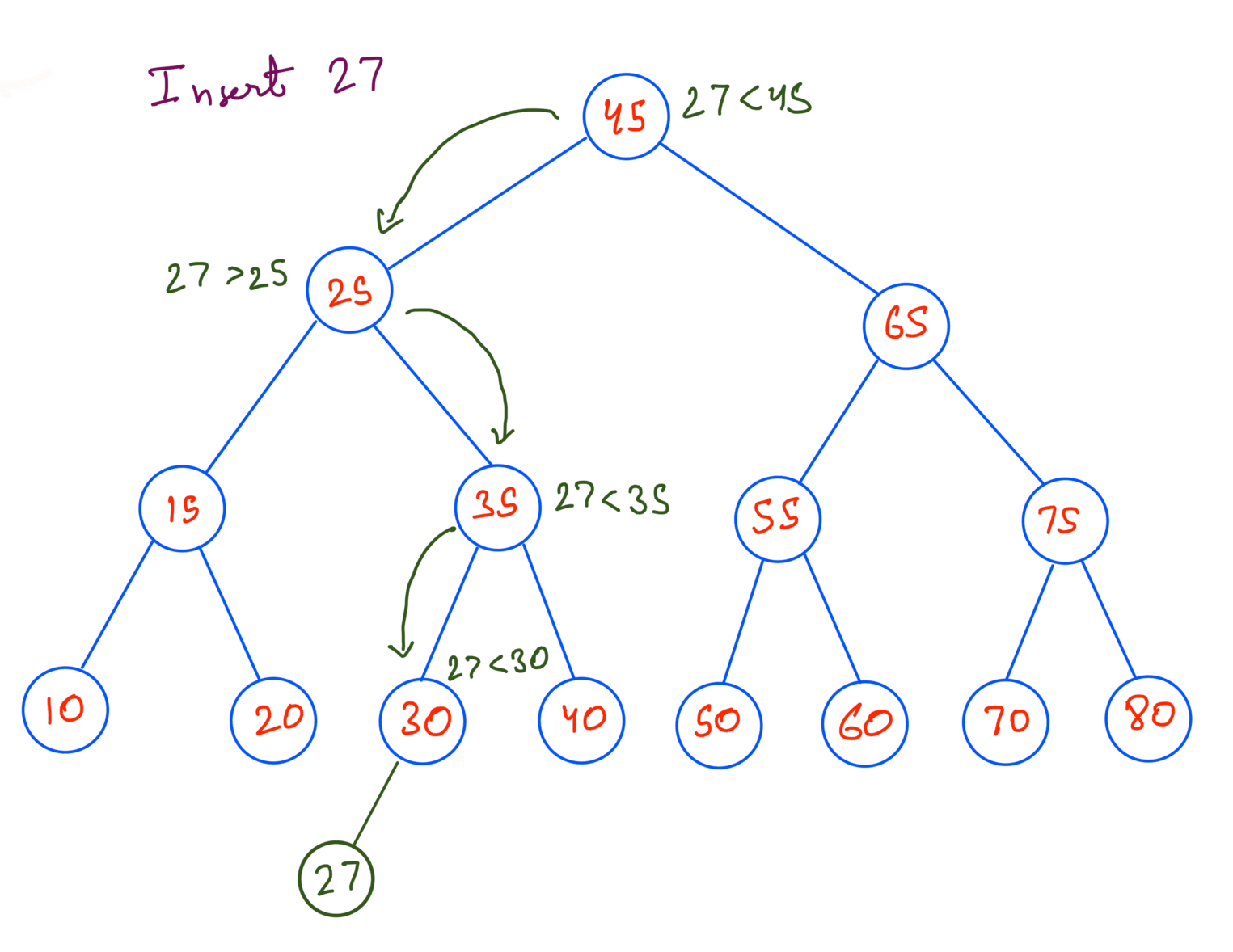
Insertion in a BST

Insertion in BST is similar to searching the value in BST. Basically we’ve to search for the place where we can insert the new value. We follow the same steps as in searching and when we’ve reached a leaf node we insert the value according to the BST property.

def insert(root, val):
  if not root:
    root = Node(val)
  elif val < root.val:
    root.left = self.insert(root.left, val)
  elif val >= root.val:
    root.right = self.insert(root.right, val)

  return root

The Time complexity is same as that for searching since we’ve to search for the position where to insert and then insert the element.

In worst case TC is O(N) for skewed BST while if BST is balanced then it’ll be O(logN).

Deletion in a BST

Deleting a value from a BST requires few extra steps after searching for the value. We’ve discussed searching for the value in previous sections. If we don’t find the value then we can return, but what to do if we found the value ?

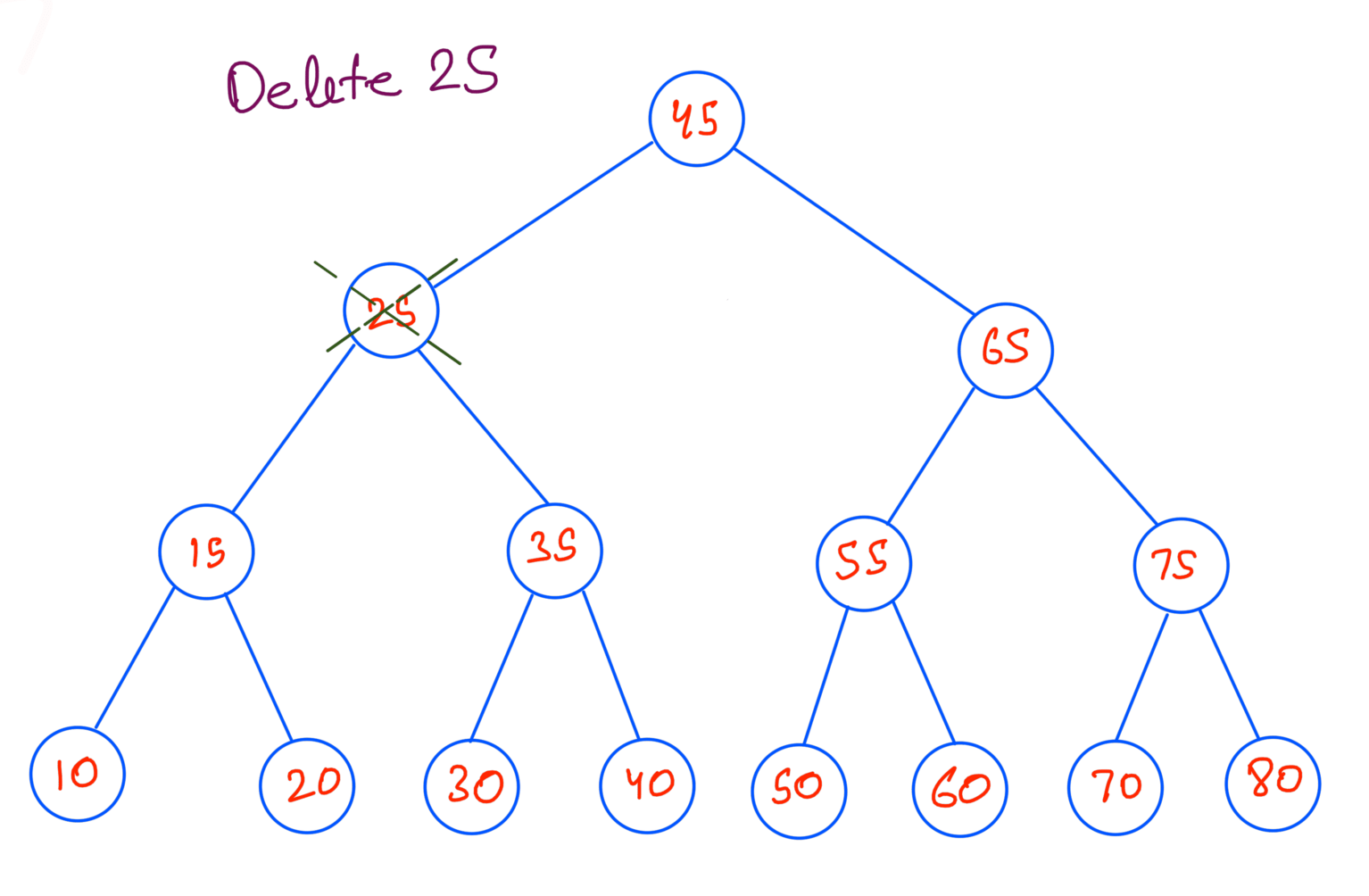
If we find the node with the value there are three cases that can happen:

1. The node has no children - In this case we can simply delete the node and update its parent to point to null.
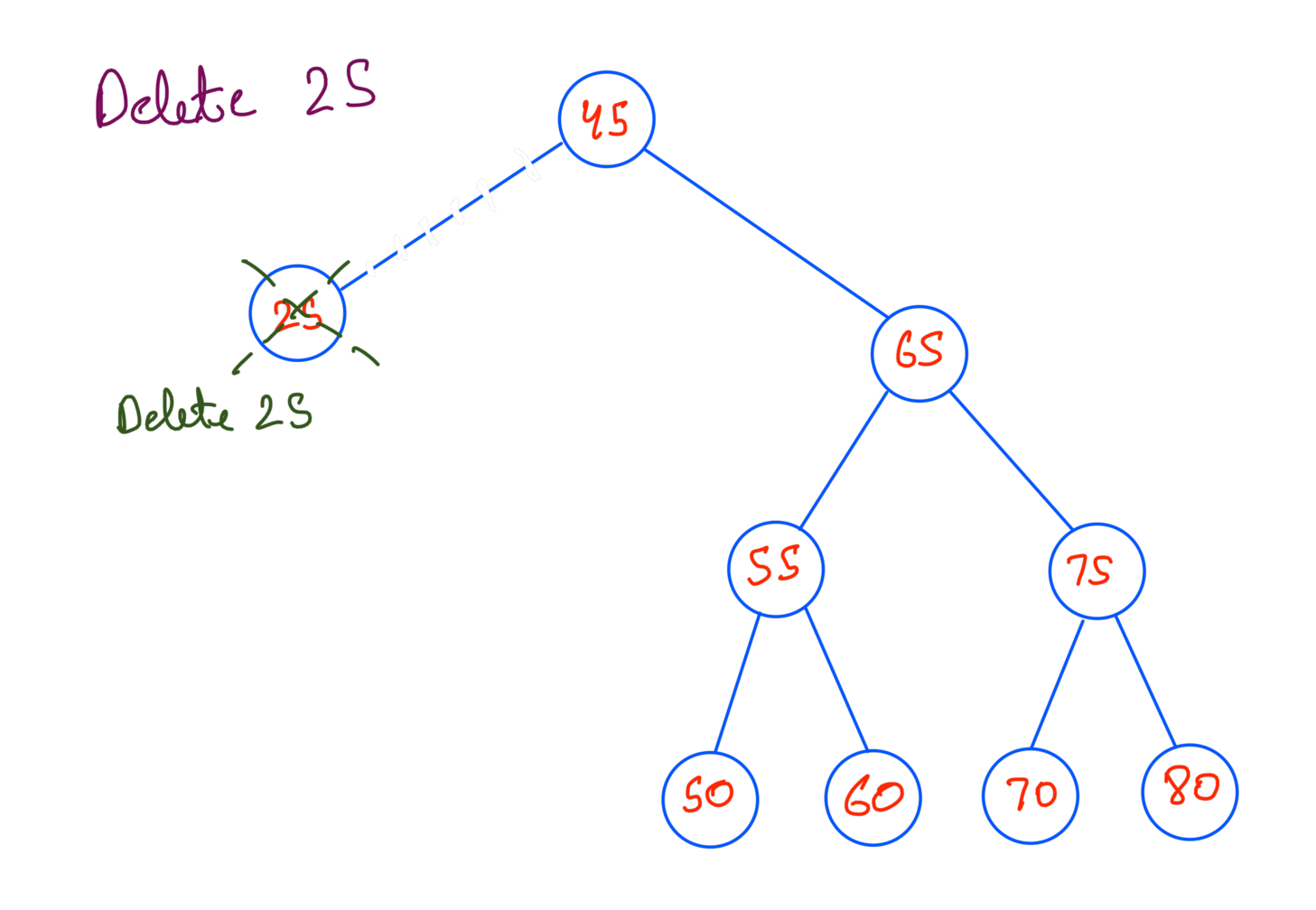
2. The node has only one child - We can replace this child with the deleted node and update its parent to point to the child node.
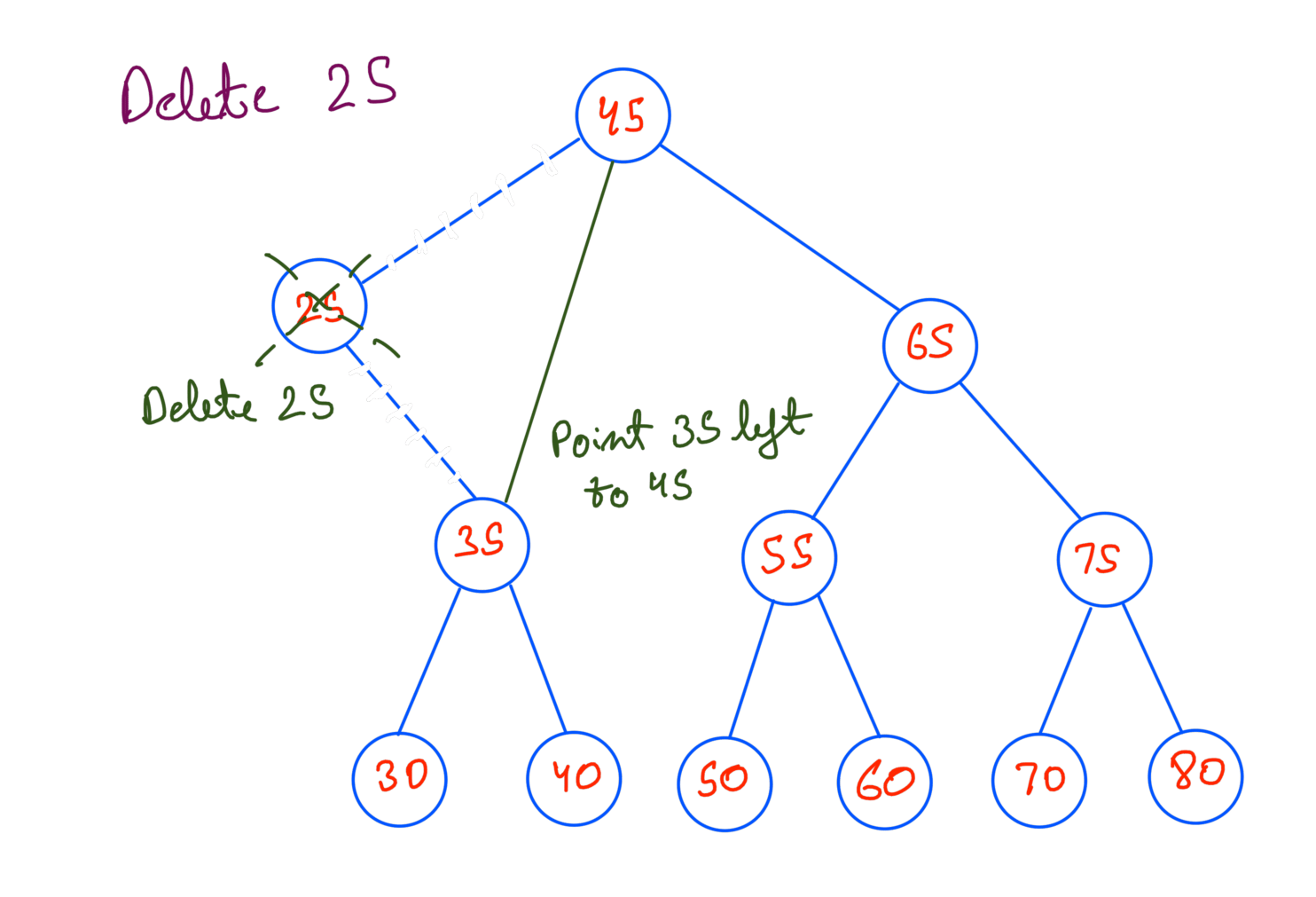
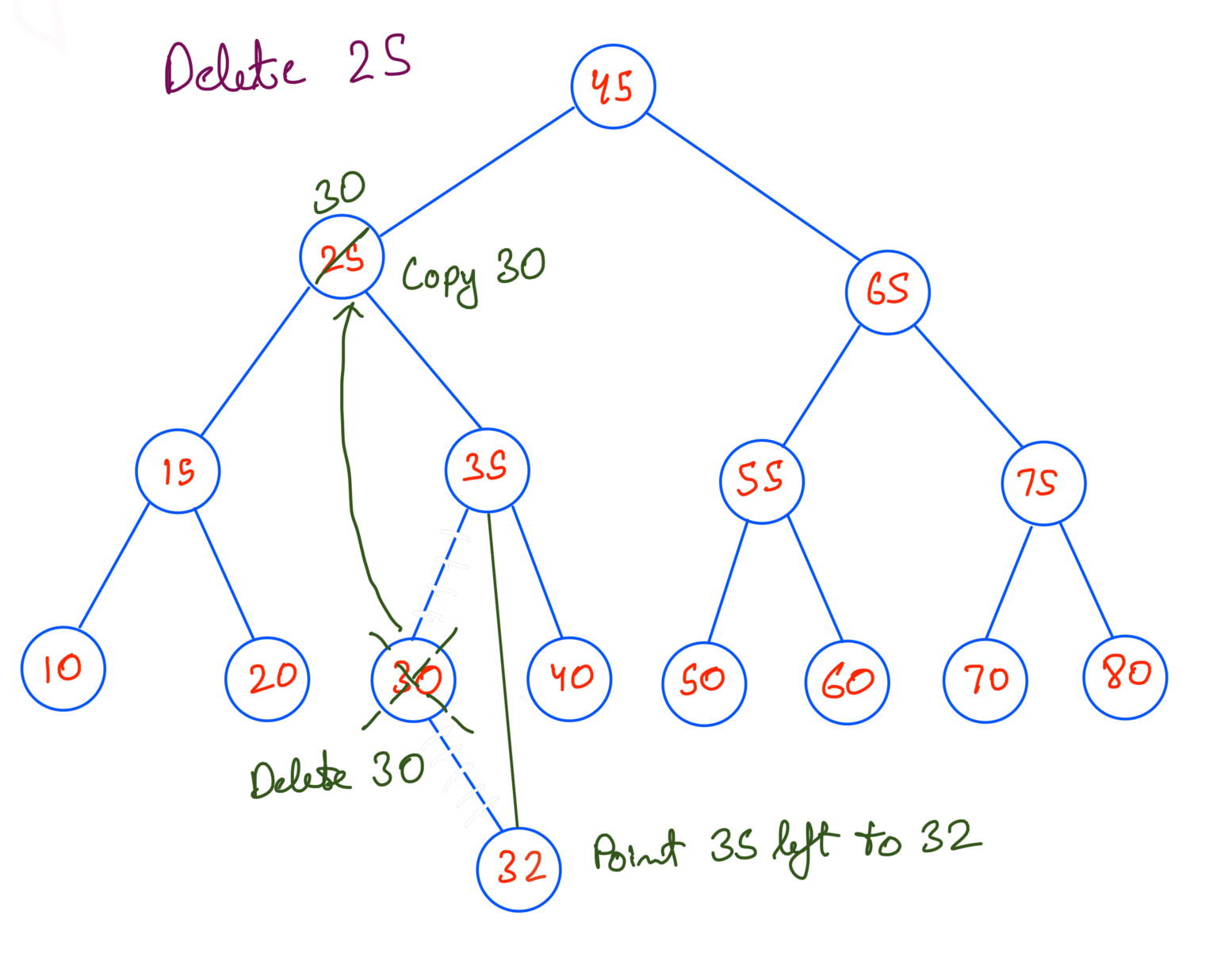
3. The node has two children - Here we can either replace the inorder predecessor or inorder successor with the value. For this case we’ll be replacing the inorder successor. To do so:

• Step 1: Copy the Inorder Successor of the node to be deleted.
• Step 2: Delete the Inorder Successor.

def delete(root, val):
  if not root:
    return None
  elif val < root.val:
    root.left = self.delete(root.left, val)
  elif val > root.val:
    root.right = self.delete(root.right, val)
  elif val == root.val:
    if not root.left and not root.right:
      return None
    elif root.right and not root.left:
      return root.right
    elif root.left and not root.right:
      return root.left
    else:
      inorder_succ = root.right
      while inorder_succ.left:
        inorder_succ = temp.left

      root.val = inorder_succ.val
      root.right = self.delete(root.right, inorder_succ.val)

  return root

TC for Deletion is same as Insert and Search, in worst case it’s O(N) for skewed BST while if the BST is balanced it’s O(logN).