A minimum spanning tree(MST) is a subset of a graph which connects all the vertices with minimum total edge weight and least number of edges(no cycles).
Formally a MST has following properties:
- Subset of the graph.
- Contains all vertices of the graph.
- Every vertex is reachable from all other vertices.
- Contains no cycles.
- Minimum total edge weight among all spanning tree.
The last point is the defining property of an MST. If we discard the last point we get a Spanning Tree which may or may not be minimum, if it satisfies the last point then it becomes an MST.
Let’s take an example graph:
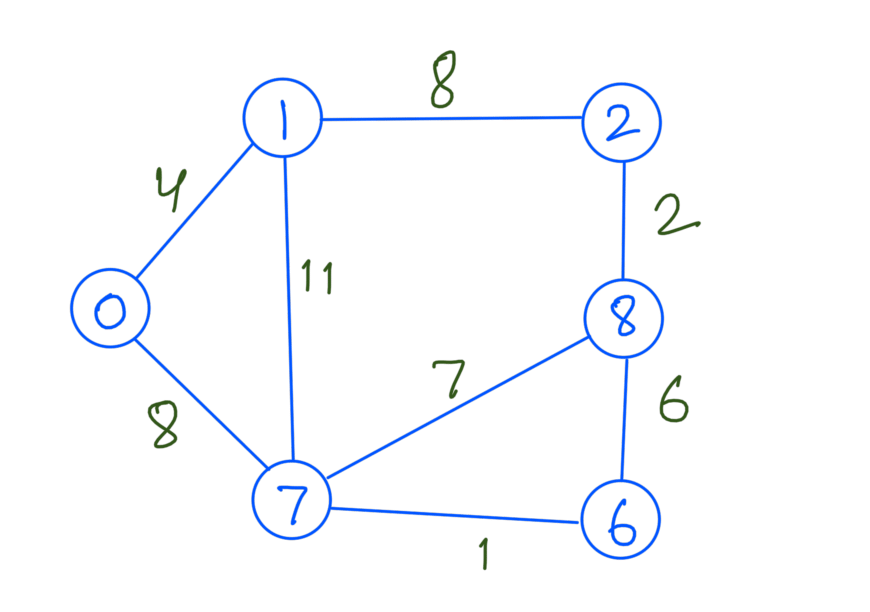
The above graph can have multiple Spanning Trees like:
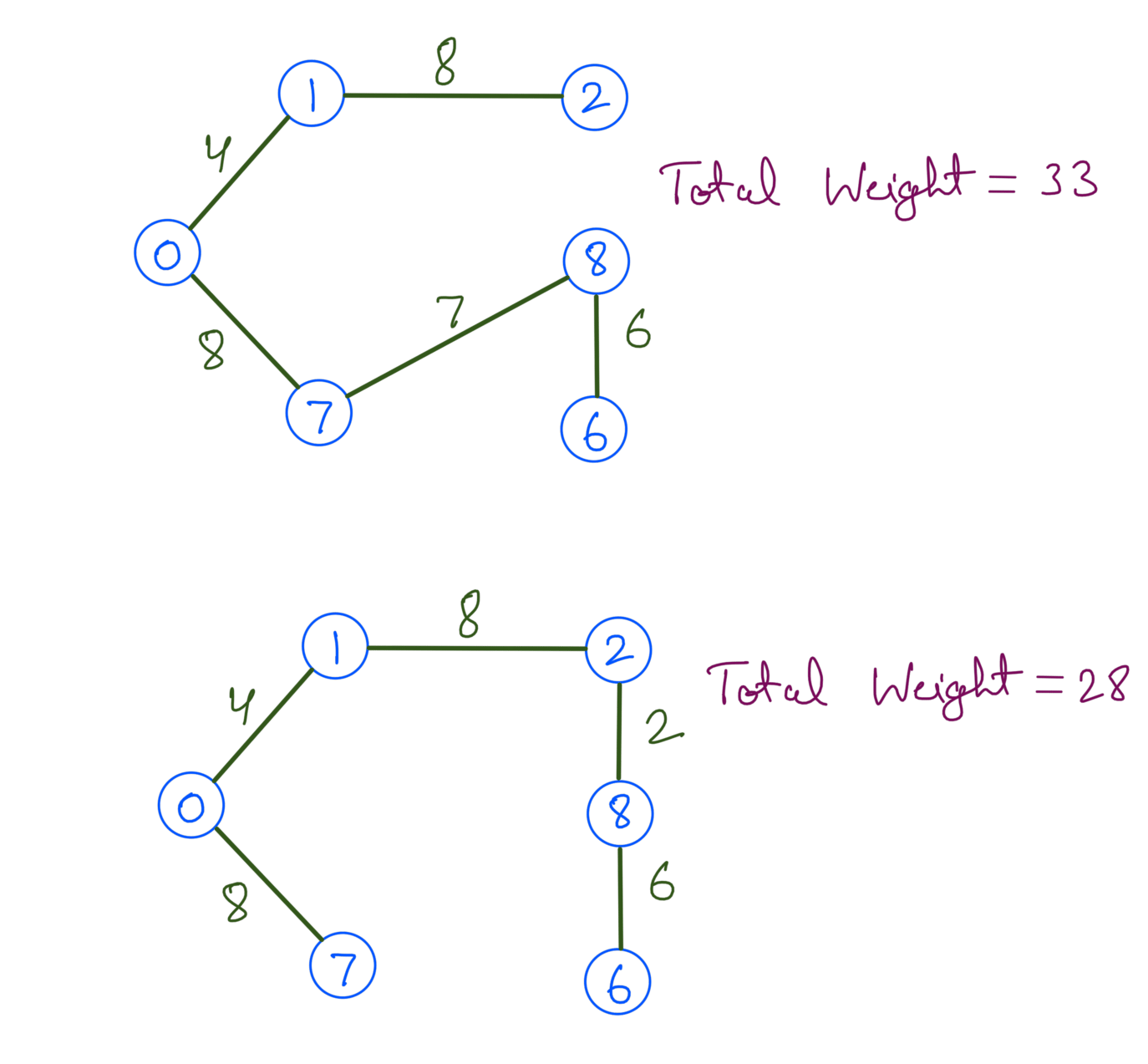
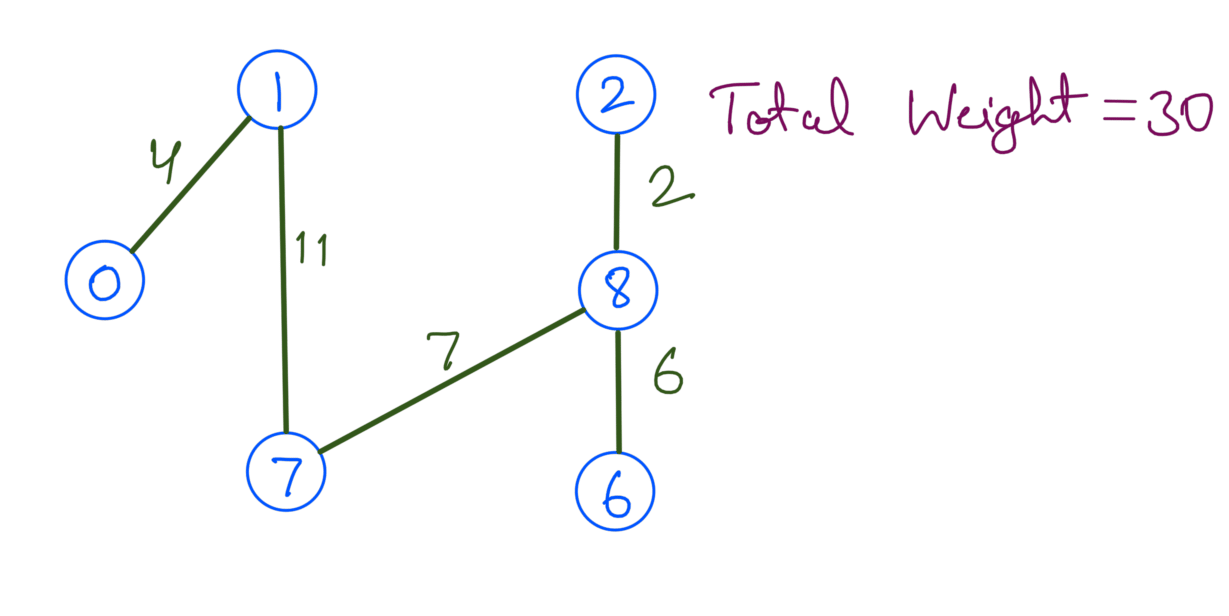
Out of the above Spanning Trees none of them is a MST since their total edge weight is not minimum. The minimum total edge weight is 23 and the corresponding MST is:
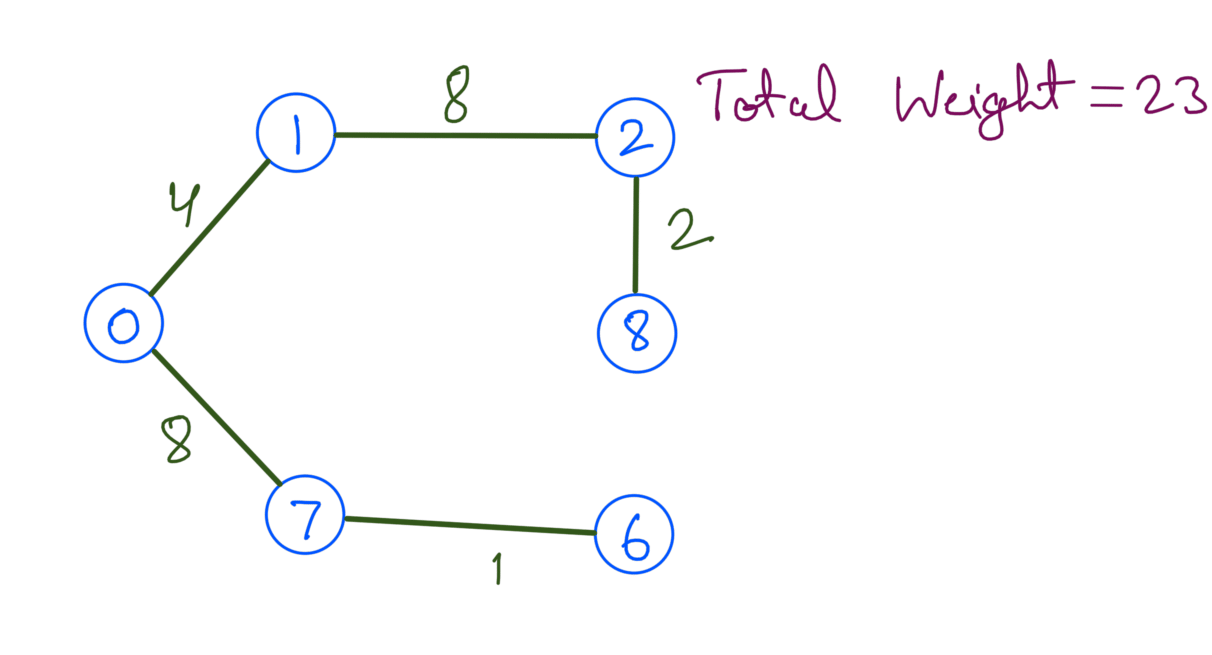
How to find MST of a graph ?
There are 2 algorithms to find MST of a graph:
- Prims’s algorithm - Prim’s finds the MST vertex by vertex while picking the least weighted edge. This way Prim’s builds the MST from the starting vertex while including one vertex at a time.
- Kruskal’s algorithm - Kruskal’s finds the MST by including the least edge every time in the graph while making sure there are no cycles. This way Kruskal’s creates a forest which finally connects into a MST.